WAIER Forum 2003: Khalid - Applications to the real world: Making mathematics enjoyable for technical students in Brunei

[ Abstract for this presentation ] [ Proceedings Contents ] [ Schedule ] [ Abstracts ]

Applications to the real world: Making mathematics enjoyable for technical students in Brunei

Madihah Khalid
Science and Mathematics Education Centre
Curtin University of Technology

There are many factors that allow students to enjoy mathematics, and students who perform better in mathematics seem to enjoy the subject more than those who are poor at it. Many students who are weak in mathematics consider the subject as boring and could not connect the mathematics that they learn in schools to the real world outside. In this paper, I will present some results of an action research that was carried out with two groups of technical education students in Brunei. The study emphasised real world mathematics application in classrooms. Other features that might enhance students' interest and enjoyment such as cooperative learning, authentic assessment and innovative activities were also part of the features included. The data of the study was mainly collected via interviews, student opinion sheet and classroom observation. The study examined students' outcome in terms of understanding and attitude.

Introduction

Student's difficulties in mathematics in general

Almost every country in the world faces problems in mathematics education. Students can be very good at the subject while others simply shy away from it. Burns (1998) has observed that more than two thirds of the American population fear and loath mathematics. One of the reasons can be attributed to the fact that, historically, mathematics has often been presented as a subject of 'absolute truths' with the existence of one correct answer to each problem (Boaler, 1994. This has intimidated students when they could not obtain correct answers. Another reason might be because mathematics traditionally has been taught in a teacher centred way and out of context, and this experience often leads to students being unmotivated and disinterested in learning mathematics.

Technical student's difficulties in mathematics

Mathematics is the key to many of the most secure and financially rewarding careers in every sector of the economy (Business Coalition for Education Reform, 1998). The impact of computers and information technology can be seen not just in engineering and science, even in such diverse areas as manufacturing and agriculture, health care and advertising. To be prepared for careers in virtually any industry, and especially for changing careers during a lifetime, secondary school students need to learn a substantial core of mathematics (Forman & Steen 1999). However, this core is like neither the abstract pre-engineering mathematics of the academic curriculum nor the restricted topics of the discredited "vocational math." New approaches are needed to meet today's challenges.

Across the international spectrum, Technical Education (or Career and Technical Education, Vocational Education, Technical and Further Education as they are known as in other countries), reflects a country's economic and social investment in education and the strategies used to enhance the skill development of workers and foster their employability (Brown, 2003b). But technical education has an image problem since parents, students and employers still hold stereotypes about it (Brown, 2003a) and therefore it does not attract high achievers. Technical/vocational studies are not able to attract academically competent students especially in mathematics and science. (Hull, 1999; Souders, 1999). Almost the same scenario exists in Brunei. Students who enrolled in technical courses have difficulty in understanding mathematics.

Mathematics has traditionally been taught in a manner that benefits abstract learners, however technical students are not abstract learners since they are more inclined to a more concrete experience. In fact Kolb (1984) and others, as quoted by Hull (1999) found out from his research that less than one fourth of students are abstract learners; most students learn best when they can connect new concept to real world through their own experiences or experiences teachers can provide them. If academics subjects such as mathematics were properly integrated with career focused courses, a student might see practical applications of mathematics contained within the academic courses (McCaslin & Parks, 2001). Again according to McCaslin & Parks (2001), a student's cognitive growth in core academic subjects should be expected to increase when technical and academic course were featured jointly. Hull (1999) believes that it is realistic to have high expectations of academic achievement from nearly all students if we restructure our learning materials and teaching to match their learning style. Classroom applications should be designed to serve mathematics -- to offer context, to illustrate use, to motivate new concepts, or to integrate topics (Forman & Steen 1999).

Issues

Work is changing in response to evolution in both employer and employee preferences, globalisation and new technology (Forman & Steen 1999). Changes are occurring in the organisation of work, the management of human resources, the relationship between technology and skill requirements, work arrangements and non-standard arrangements (self-employment, part-time work, etc.). The preparation of workers for entry into and advancement in the workplace of the next decade requires an educational program that provides not only job skills, as career and technical education did throughout the 1900s, but also higher order thinking, problem solving, and collaborative work skills. With the advancement of technology and the dependence of jobs on information technology, there is a greater need for educators to examine the kinds of mathematics that students need. An understanding of mathematics has become more crucial than before. The increasing number of students pursuing their studies for higher degree makes it important for technical institution to provide curriculum that should be designed to make articulation possible between technical and vocational education and higher education (Saluja, 1993). Therefore, there is an urgent need for technical institution to:

Prepare able work force to meet current needs and characteristics
Existing jobs currently demand substantial skills from employees. Trent (1999) state that while nearly 3 out of 4 workers in the USA are employed in occupations that require education and training below the associate's degree level, the demand of better skilled workers increases every day. A recent survey of work establishments report that restructuring and the introduction of new technology has increased the skills demands for non-managerial employees (Trent, 1999). Current work force are expected to be able to apply skills and theo ries to the real world, able to think at a higher level, able to work collaboratively (in other words can be an effective team player) and have the necessary soft skills (interpersonal and human relations skills like the ability to listen and communicate well).
In the Brunei context, as the country gears towards industrialisation, the demand of able workforce is becoming more and more urgent. The 2002 figure showed (APEC, 2002) that almost half of the work forces were employed in mining and manufacturing (industry). The government has tried to reduce the reliance on foreign workers and will gradually replace the number of foreign work force which account for 60,000 of about a total of 140,000 workers with locals.
Prepare students ready to pursue higher education
At stake is nothing less than the fundamental nature of school mathematics: its content (what should be taught), pedagogy (how it should be taught), and assessment (what should be expected). Students have realised the competitiveness that they will face when they are ready to join the work force. More and more of the students now would continue to pursue their study to a higher level after getting their Diploma, the latest figure showing about 20% of Diploma graduates (report, 2002). Mathematics at the higher levels is more rigorous and need a strong understanding of the basics. Since many of the students who enrolled for the diploma course are not mathematically strong, it is important that they be equipped with a deep understanding of mathematical concepts and a rigorous syllabus, not the watered down syllabus as was introduced previously.
What should be considered are the content (what should be taught), pedagogy (how it should be taught), and assessment (what should be expected). I believe, with the right approach, students could be good and interested in mathematics. By highlighting the rich mathematics embedded in everyday tasks, this approach (in contrast to traditional "vocational math") can dispel both minimalist views about the mathematics required for work and elitist views of academic mathematics as an area with little to learn from work based problems.

Considering these two issues, curriculum developers and instructors are faced with the dilemma of balancing between preparing students for immediate employment, where they need a more hands on and concrete approach to mathematics, and preparing students for further studies, where conceptual understandings are needed. At the same time, problem solving capabilities are essential.

Making mathematics meaningful

Those who discuss mathematics education frequently describe mathematical knowledge in broad categories such as skills and understanding, concepts and facts, procedures and practices, or insights and knowledge. Whole volumes of educational research are devoted to distinguishing among these different aspects of mathematical knowledge (Copa & Wolff, 2002). The standards movement in the USA has tended to subsume all these distinctions into two categories of knowledge and performance: what students should know and what students should be able to do (Ravitch, 1995; Tucker & Codding, 1998).

The two broad cultures of mathematics education argue with each other largely because they differ in the interpretations they give to these different aspects of mathematical knowledge. Those who favour the traditional curriculum centred on algebra, functions, and Euclidean geometry argue that mastery of facts and basic skills are a prerequisite to understanding and performance. Reformers who favour a broader curriculum take a more constructivist view - that understanding and mastery are an outgrowth of active engagement with contextualised mathematics (Copa & Wolff, 2002).

Mathematics is supposed to follow the path of variations that reflect its grounding in authentic problems. However, by embedding mathematics in practice, mathematics can offer students both theory and know how. The logical structure that unites mathematics guarantees that all understanding, no matter how specific, has the potential to enhance mastery of other areas. Topics in mathematics may be chosen for proximate utility, their study can provide insight and understandings sufficient for lifelong learning (Copa & Wolff, 2002).

A curriculum for mathematics requires appropriate content, authentic contexts, engaging tasks, and active instruction. By featuring mathematics in common contexts, a curriculum can motivate students to link meaning with mathematics. The best problem settings offer opportunities for exploration from multiple perspectives, including graphical, numerical, symbolic, verbal, and computational. Technology - from graphing calculators and word processors to spreadsheets and symbolic algebra systems, can enhance understanding from each of these perspectives. Effective contexts provide opportunities for horizontal linkages among diverse areas of life and work as well as vertical integration from elementary ideas to advanced topics. Experience with rich contexts helps students recognise that asking questions is often as important as finding answers. Such contexts invite variations that can stimulate mathematical habits of mind and propel students to deep understanding (Forman and Steen, 1999).

Current trends in technical education

Historically, vocational and technical curricula that were designed to prepare students for work have been looked down as second class status in comparison with the more rigorous academic curricula. Too often, vocational programs became dumping grounds for students who appeared slow or unmotivated - "the lower achievers." Most programs responded by limiting goals and lowering expectations, thereby offering stunted education to students who were already behind. In contrast, contemporary career oriented curricula have been designed not primarily as training for low skill jobs but as motivation for rigorous study, both academic and vocational (Bailey & Merritt, 1997; Hoachlander, 1997). Vocational mathematics too has provided only a narrow range of skills limited to middle school topics and devoid of conceptual understanding (National Center for Education Statistics [NCES], 1996). Such programs leave students totally unprepared - not only for modern work and post-secondary education, but even for advanced secondary school mathematics.

Traditionally, mathematics is one of the subjects that is learned alone. Lectures are the dominant mode of teaching and homework is done alone at home. Group projects are few. Teaching for understanding - the primary goal of mathematics and science education reform - requires that students are actively engaged in the classroom, are willing and able to communicate their ideas, and are able to learn from each other. Abstract learners benefited from the traditional approaches but most technical students are not abstract learners (Hull, 1999). They are more at home with the concrete style of learning and process information actively (by doing) because of the nature of the technical courses that are more hands on.

The trend in technical education nowadays is to integrate academic and technical skills. For nearly a decade, the "applied academics" movement demonstrated that students who had performed poorly in abstract mathematics courses could achieve high levels in those subject areas if they are taught in applied or hands on format (Hull, 1999). This might had been due to the fact that not all student are abstract learners, but that some are concrete learners and they process information actively and not reflectively (Kolb, 1984). Many of the technical students were found to belong to the latter category. Because of the changing nature of today's workplace, and the nature of jobs becoming increasingly complex, students must be offered technical studies that provide strong academic skills. They will need to apply these academic skills and theories to the problems that they will encounter in the real world. Technical education in today's world must create opportunities for students to learn in real world contexts and also exp ose students to the wide range of career paths available to them (Bottoms, undated). By exploring mathematics via tasks which come from workplace and everyday settings, and with the aid of common tools like spreadsheets, students are more likely to see the relevance of mathematics and are more likely to learn it in ways that are personally meaningful than if it is presented abstractly and applied later only when time permits (Taylor, 1998). In fact, according to (Forman & Steen, 1999), all mathematics standards in USA argue or imply that learning is enhanced when embedded in rich, authentic contexts; when students engage with each other and with the world around them, and when students are expected to experience, explore, and explain.

The above sentiments coincide with the recommendations of the current mathematics curriculum for National Diploma Year 1 that was introduced in Brunei in November 1999. It was implemented in early 2000 and:

Encourages the development of thinking skills through an intuitive rather than rigorous instructional approach.
Emphasises on the integration with other subject disciplines and learner directed application of skills
States that learning and assessment throughout will be work related. (Programme-Guide, 1999)

Summarising the sentiment of what was said above, I conclude that mathematics lessons for technical students should have to consider the following aspects. Lessons should:

Integrate academic and technical subjects
Emphasise technology in learning
Contain elements of cooperative Learning
Be academically rigorous and career relevant
Emphasise soft skills
Be taught in context to the authentic real world of life and work

Background of study

Two classes of students in their first year of National Diploma in various courses were introduced to an innovative way of teaching, having the characteristics mentioned before. In the classrooms, besides introducing the reform approach, I also tried to conform to the preferred classroom environment identified by the students before. Addressing the preferred classroom environment identified, I tried to be more supportive, students were put in groups of four for them to work cooperatively, relevance were emphasised in mathematics teaching, teaching are made more innovative by various kinds of activities and assessment and more on task orientation is emphasised. As for the theme of learning, emphasis is on the application to the real world. Each example and problems are connected to the real world and are relevant to the students' course of study.

The two classes mentioned were ND/ELE/10 (National Diploma in Electrical and Electronics Engineering) and ND/RTE/08 (National Diploma in Radio, Television and Electronics Engineering). These two classes were taught using a package on the topic of Trigonometry, designed and developed by the author in accordance to the ideas discussed before. The package implementation took two months to be completed.

Aims of study

Previous research has established that attitudes toward mathematics impacted on mathematics achievement or was correlated with mathematics achievement (Gadalla, 1999); (Simich-Dudgeon, 1996); (Lokan & Greenwood, 2000); (Odell & Schumacher, 1998), (Kim & Hocevar, 1998); (Weinberg, 1995). This study looked at the impact of changing classroom environment (in terms of instructional or pedagogical context) on attitude and mathematics achievement.

The aims of this study were to:

Implement innovative teaching and learning methods to improve students' mathematical understanding and motivation and interest in mathematics
Demonstrate relevance of mathematics in the real world and workplace to enhance students' mathematical understanding and motivation/interest
Incorporate the preferred classroom environment components that was identified by the students in the reform approaches
Provide ideas to other instructors about alternative/authentic assessment to have more variation in assessment approach

Methodology

A mixed qualitative and quantitative methodology approach was adopted for the research. To measure the cognitive achievement of students before and after the implementation of the package, pre-test and post-test were used. Classroom observation and interviews were also carried out during the implementation.

To measure the affective achievement of the students, two surveys were given both before and after the implementation. To identify students' actual and preferred classroom environment, classroom environment surveys named CCEI were administered. The scales included in the classroom environment survey were Student Cohesiveness, Teacher Support, Involvement, Innovation, Cooperation, Innovation, Task Orientation, Individualisation and Relevance. To measure students' attitude towards mathematics, a survey with scales Enjoyment & Interest, Relevance and Importance were given out at the same time as the classroom environment survey, both before and after the implementation of the package. Interviews with teachers and students were also carried out during these surveys.

Implementation

The students in each class were divided into groups of three or four each. They were given tasks and activity sheets and are supposed to work as a group. They are expected to discuss, argue and interact among themselves while engaged in doing the activities. They are also expected to present the solution of the problems to the class.

Examples of the real world approach are as follows:

For the topic of radian measure, the problem of measuring the earth's radius was given. This problem was similar to the problem solved by Eratosthenes of 240 BC (also known as the Noon Project on the Internet).
For the topic of trigonometric ratio, the activity that were given out was to find the width, pitch, height and angles of a given roof and to find one measurement when other measurements were given. Because these students are electronics engineering students, they were also required to find the shortest route to wire an antennae on the roof from inside a given house.
For the topic of trigonometric graph, a project named "Trigonometric Graphs Around Us" was given. Students were required to look at one phenomenon around them that exhibit a trigonometric graph, collect the data, graph them, find the equation of the graph and finally use it to prove other readings.
For the topic of sine and cosine rule, various authentic, real world problems were solved in groups.

All of the activities mentioned above have been identified to benefit the learning of mathematics to the technical students, as they satisfy the following traits:

Relevance - learning and assessment to be work related (connect to everyday, real world situation)
Integrated with the technical field
Cooperative or group learning
Use technology as far as possible
Encourage development of thinking skills through intuitive approach

Results

The results shown below have been divided into two different classifications, that is the cognitive and the affective achievement.

Cognitive achievement

Figure 1 shows the result of the pre- and post-tests that were given before and after the implementation of the reform approaches. There was a significant increase in scores for the ELE class whereas the RTE class shows a minimal change in score. The pre- and post-test were set to be parallel in nature. The only difference is that the post -test was set to include more application problems that were connected to the real world and required more thinking skills. No prior notice was given before both tests were administered.

Figure 1: Graph of pre and post test scores for the ELE and RTE classes.

Affective achievements

In measuring the affective achievement of the students, two types of surveys were used. One measured the perceived learning environment and the other m easures the attitude of students towards mathematics. Using the pre/post surveys, students perceived learning environment and attitude could be measured and compared.

Attitude toward mathematics

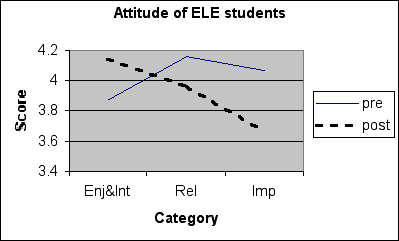
Figure 2: Graphs showing attitudes towards mathematics surveyed before and
after the implementation of the reform approaches for ELE class.

Figure 2 and 3 shows the result of a survey on students' attitude towards mathematics. The survey measured the attitude according to three main categories, namely Enjoyment & Interest, Relevance and Importance. The relevance category contained statements about the relevance and use of mathematics in the real world and to the students' course of study whilst the importance category contains statements about the importance of mathematics in life.

Figure 3: Graphs showing attitudes towards mathematics surveyed before and
after the implementation of the reform approaches for RTE class.

From the figure we could see that for the ELE class, there was a significant increase in perceived enjoyment and interest of the students towards mathematics while there was a significant decrease in the relevance and importance category. This decrease, in my opinion was due to about three students who do not seemed happy with the way the class was conducted. Because of the small nature of the sample, these three students' opinion affected the result of the survey. I conducted an interview with one of these students who happened to be a mature "in service" student (who came back to study for her diploma after working with the government department), and according to her, she considers the activities that we did were a waste of time. She preferred the traditional way where a formula would be give to work on the problems given in class.

For the RTE class, there was no change in attitude in the categories of Enjoyment & Interest and Relevance but there was a slight increase in the Importance category.

Classroom environment

Figure 4: The results of the pre and post learning environment survey for the ELE class.
The scales 1 = Student Cohesiveness, 2 = Teacher Support, 3 = Involvement, 4 = Innovation,
5 = Cooperation, 6 = Task Orientation, 7 = Individualisation, 8 = Relevance

Figure 4 shows that there was a significant increase in the individualisation scale and a decrease in the student cohesiveness scale for the post actual survey. In other scales, there is only minimal increase and in fact there is a slight decrease in the relevance scale.

Meanwhile Figure 5 of the learning environment for the RTE class shows a significant increase in the individualisation and teacher support and notable increase in student cohesiveness scale. There is only minimal increase in other scales.

Figure 5: The results of the pre and post learning environment survey for the RTE class.
The scales 1 = Student Cohesiveness, 2 = Teacher Support, 3 = Involvement, 4 = Innovation,
5 = Cooperation, 6 = Task Orientation, 7 = Individualisation, 8 = Relevance

Discussion and conclusion

From the results above, we could see that there has been some increase in terms of cognitive and affective achievement for both classes although their level of increase differs. The ELE class which has a higher cognitive achievement, only exhibit a small increase in cognitive achievement but the RTE class, with the modest increase in understanding exhibit a bigger change in affective increase. For these two cases, it can be said that changes in instructional approach and in learning environment did change both the cognitive and affective achievements. The emphasis on more application to the real world seemed to be effective in increasing students' cognitive and affective achievements. Instructional theories should be encouraged in a wide variety of different areas - not just in the cognitive domain where we need theories for fostering understanding, building higher order thinking skills, developing metacognitive skills, designing problem based and interdisciplinary or thematic learning environments, and tailoring instructional guidance to specific content area idiosyncrasies. Similarly for the affective domain, where we need guidance for developing what Daniel Goleman calls "emotional intelligence" and for what Thomas Lickona calls "character education," as well as how to develop attitudes and values and so forth (Reigeluth, 1999).

As was commented earlier, not all students favour the instructional changes that concentrate on students' activities and exploration. The mature students who were comfortable with the traditional way of teaching seemed to resist changes. In my opinion, these students require more time to get use to a different instructional approach and the period of two months that they have is not enough to foster changes in their attitude.

Changing the learning environment to suit the ones preferred by the students has produced changes in both type of achievement measured.

References

Bailey, T. R., & Merritt, D. (1997). School-to-work for the college bound. Education Week, 29 October, 32-37.

Bottoms, G. (undated). Professional Teaching Standards for Career/Technical Educators. SREB - High Schools that Work. [viewed 27 June 2003] http://www.sreb.org/programs/hstw/career/ProfessionalStandards.asp

Brown, B. L. (2003a). The image of career and technical education. ERIC/ACVE Publication: Practice Education Brief No. 25. [viewed 10 June 2003] http://ericacve.org/docgen.asp?tbl=pab&ID=115

Brown, B. L. (2003b). International models of career-technical education. Trends and Issues Alert No. 42. ERIC Clearinghouse on Adult, Career and Vocational Education. [verified 22 Oct 2003] http://ericacve.org/docgen.asp?tbl=tia&ID=165

Copa, G. H., & Wolff, S. J. (2002). New Designs for Career and Technical Education at the Secondary and Postsecondary Levels: Design Guide for Policy and Practice. St. Paul, Minnesota: National Research Center for Career and Technical Education University of Minnesota.

Forman, S. L., & Steen , L. A. (1999). Beyond eighth grade: Functional mathematics for life and work.. Berkeley, CA: National Center for Research in Vocational Education. [verified 22 oct 2003] http://www.nccte.org/publications/ncrve/mds-12xx/MDS-1241.asp

Forman, S. L., & Steen, L. A. (1999). Making Authentic Mathematics Work For all Students. In A. Bessot & J. Ridgway (Eds.), Education for Mathematics in the Workplace. Dordrecht, Netherlands: Kluwer Academic Publishing,.

Gadalla, T. (1999). A comparison of the factor structure of boys' and girls' responses to the TIMSS mathematics attitude questionnaire. Paper presented at the American Educational Research Association, Montreal, Canada.

Hull, D. M. (1999). Teaching mathematics contextually: The cornerstone of Tech Prep. Waco, Texas: CORD.

Kim, S., & Hocevar, D. (1998). Racial differences in eighth grade mathematics: Achievement and opportunity to learn. Clearing House, 71, 175-178.

Kolb, D. A. (1984). Experiential Learning: Experience as the Source of Learning and Development. Englewood Cliffs, NJ: Prentice-Hall, Inc.

Lokan, J., & Greenwood, L. (2000). Mathematics achievement at lower secondary level in Australia. Studies in Educational Evaluation, 26, 9-26.

McCaslin, N. L., & Parks, D. (2001). Teacher education in Career and Technical Education: Background and Changes for the new milleneum. Journal of Vocational Education Research, 27(1).

Odell, P. M., & Schumacher, P. (1998). Attitudes towards mathematics and predictors of college mathematics grades: Gender differences in a 4-year bussiness college. Journal of Education for Business, 74, 34-38.

Programme-Guide (1999). Mathematics for National Diploma 1. Programme Development Section, Department of Technical Education. Brunei Darussalam.

Reigeluth, C. M. (1999). What Is the New Paradigm of Instructional Theory. Lawrence Erlbaum Assoc.

Saluja, S. (1993). Philosophy, objectives, development, implementation experience and evaluation of curriculum for Technical and Vocational Education (ED/93.C/20). Turin, Italy: UNEVOC, Unesco.

Simich-Dudgeon, C. (1996). Ethnicity, gender, attitudes and mathematics achievement: The 1992 NAEP trial state assessment. Paper presented at the American Educational Research Association, New York, NY.

Taylor, J. E. (1998). The importance of workplace and everyday mathematics. Ch 4 in High School Mathematics at Work: Essays and Examples for the Education of All Students. Washington, DC: National Research Council. [viewed 20 June 2002, verified 22 Oct 2003] http://books.nap.edu/html/hs_math/ch4.html

Trent, W. T. (1999). The changing nature of work and its implications. Institute of Government and Public Affairs Publication. [viewed 2 Oct 2003] http://www.igpa.uillinois.edu/publications/critIssues/work.pdf

Weinberg, M. (1995). Gender difference in students attitude towards science: A meta-analysis of literature from 1970-1991. Journal of Research in Science Teaching, 32, 387-398.

Author: Madihah Khalid
Science and Mathematics Education Centre
Curtin University of Technology
khalidm@ses.curtin.edu.au
Please cite as: Khalid, M. (2003). Applications to the real world: Making mathematics enjoyable for technical students in Brunei. Proceedings Western Australian Institute for Educational Research Forum 2003. http://www.waier.org.au/forums/2003/khalid.html

[ Abstract for this presentation ] [ Proceedings Contents ] [ Schedule ] [ Abstracts ]
Created 22 Oct 2003. Last revised 19 May 2006. URL: http://www.waier.org.au/forums/2003/khalid.html
The Forum Proceedings are © Western Australian Institute for Educational Research. However
the copyright for each individual article remains with the authors of the article.
HTML: Roger Atkinson and Clare McBeath